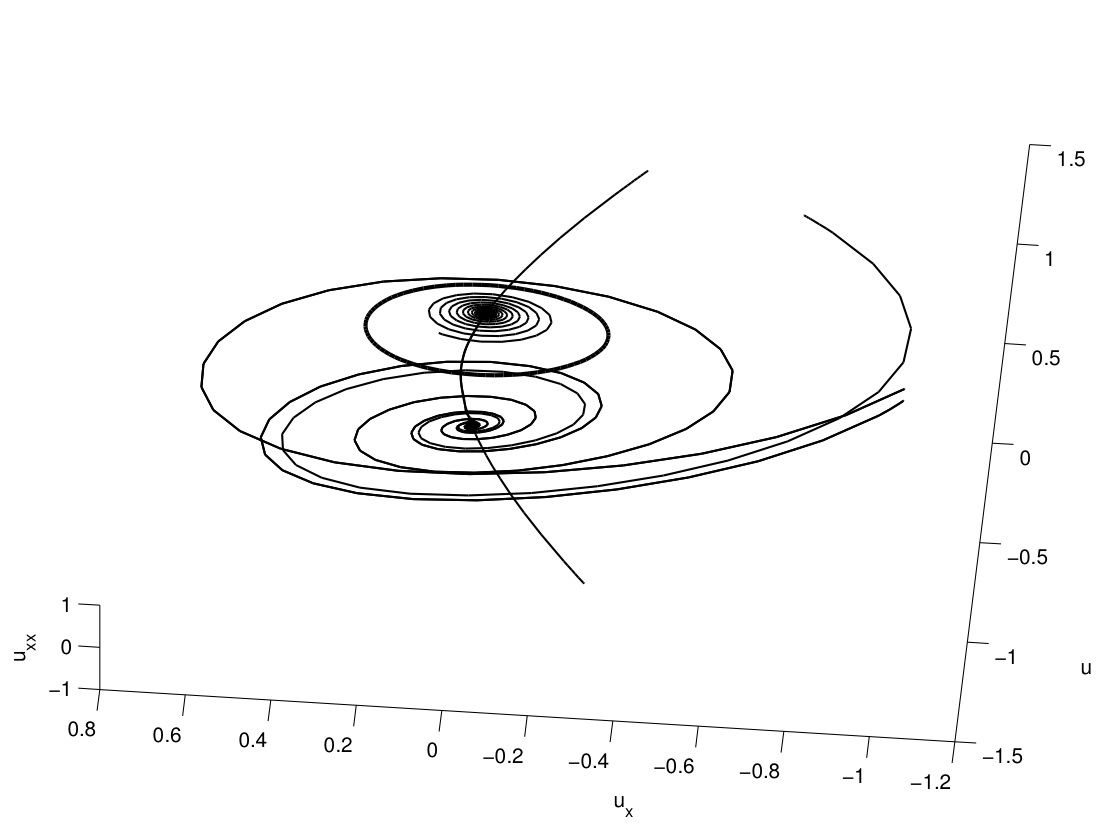
The Kuramoto-Sivashinsky equation a partial differential equation (PDE), is a canonical model for pattern formation, arising in such varied applications as plasma dynamics, propagation of flame fronts, inclined thin film flow, and turbulence. One interesting class of solutions consists of periodic traveling wavesu(x,t)=\bar u(x-ct): periodic wave-forms propagating at speed c without changing shape. These satisfy the simpler ordinary differential equation (ODE) -cu+ \frac{1}{2}u^2 + \delta u'+ \epsilon u'' + u''' = q \,, where q is a constant of integration. By various changes of coordinates, we may arrange that \epsilon\ge 0 and c=0, further reducing the problem. In the picture above, we display the three-dimensional phase portrait of this traveling-wave ODE for c=0, q=0.4, showing the trajectories of various solutions in coordinates(u,u',u'')=(u,u_x,u_{xx}): in particular, the two equilibria (u,u',u'') \equiv ( \pm \sqrt{2q},0,0), their stable and unstable manifolds, and a closed loop corresponding to a periodic solution. This is part of a two-dimensional surface of such periodic orbits as c and q are varied.

Spectral vs. nonlinear stability 

It has been known since shortly after the introduction of this model in [Y. Kuramoto and T. Tsuzuki, "On the formation of dissipative structures in reaction-diusion systems", Progress of Theoretical Physics, 1977] and [G.I. Sivashinsky, Nonlinear analysis of hydrodynamic instability in laminar flame. I. Derivation of basic equations, Acta Astron., 1977] that, fixing without loss of generality speed c=0 (stationary solutions) and varying q, one obtains a band of spectrally stable waves; see [B.I. Cohen, J.A. Krommes, W.M. Tang, and M.N. Rosenbluth, Nucl. Fusion 16,6, 1976] and [U. Frisch, Z.S. She, and O. Thual, Viscoelastic behaviour of cellular solutions to the Kuramoto{Sivashinsky model J. Fluid Mech. 168, 1986].

However, it has been a long-standing open problem whether or not this known spectral stability, which pertains to the linearization of (1) about a periodic solution, translates to nonlinear stability, or stability of solutions of (1) itself. The solution of this problem, obtained by Blake Barker, Mat Johnson, and Kevin Zumbrun of IU together with Pascal Noble and Miguel Rodrigues of University of Lyon has recently been announced. The method of solution was developed as part of a larger project on modulational stability of periodic solutions of conservation and balance laws initiated in the early 2000's with former student Myunghyun Oh.

All figures prepared by Blake Barker, using SpectrUW and MATLAB numerical packages.- Kevin Zumbrun