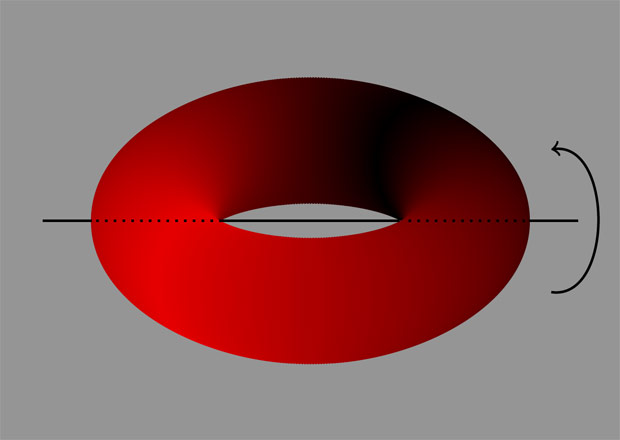
The torus has a symmetry of period 2 given by a 180° rotation about the axis in the picture. This symmetry has 4 fixed points. Less obvious is a symmetry of period 3 with exactly 3 fixed points. This period 3 symmetry is harder to see because the abstract torus cannot be arranged in 3-space to show the symmetry as a restriction of a symmetry of space.

In topology, the theory of transformation groups is the study of the symmetries of geometric objects such as manifolds. Some manifolds, like a round sphere, have so much symmetry that they are perhaps boring. Other higher dimensional manifolds have no symmetry at all. The fixed point set is perhaps the most immediate tool to use in the classification of symmetries.

P.S. Hint for "seeing" the period 3 symmetry: show that the torus can be realized as a hexagon with opposite sides identified and consider the symmetry corresponding to a 2π/3 rotation of the hexagon.- Allan Edmonds