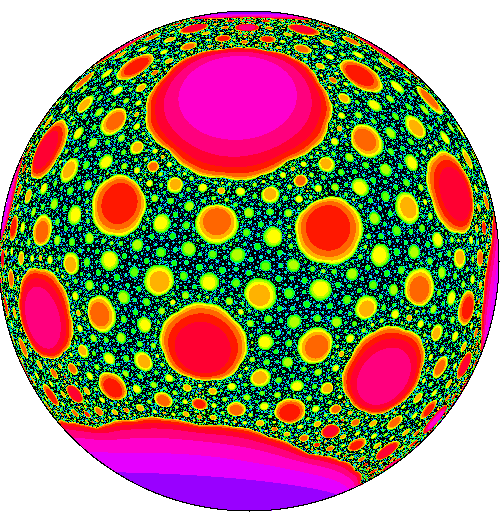
The dark region shows an approximation of the ''fractal'' Julia set of a certain cubic rational function, drawn here on the Riemann sphere. The complementary colored regions form a countable collection of open disks in which (i) each boundary is a simple closed curve, (ii) the closures of no two distinct disks intersect, (iii) the diameters of the disks tend to zero. 

By a theorem of Whyburn, this Julia set is then homeomorphic to the well-known Sierpinski carpet, a subset of the plane obtained as follows: Divide the unit square into nine congruent squares, and remove the open middle square. Do the same to the remaining eight squares, and iterate. The Sierpinski carpet is universal in the sense that it contains a homeomorphic copy of any planar one-dimensional continuum. The Julia set here and the Sierpinski carpet enjoy the additional metric property of having area zero and Hausdorff dimension strictly less than two.- Kevin M. Pilgrim