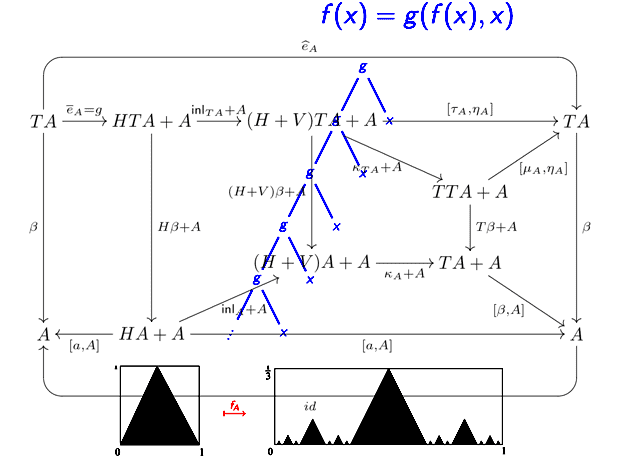
Consider the equation f(x) = g(f(x),x). This defines f(x) in terms of itself, and it falls under the rubric of recursion. If we take g to be a function symbol with no interpretation, then we can take the solution f(x) to be the tree shown in blue. But we might also start with one or another fixed interpretation of g. For example, let "A" be the complete metric space of compact subsets of the unit square. We might take

g: A -> A

to be given by

g(S,T) = (1/3)S union ((1/3) T + (1/3)) union ((1/3)S + (2/3))
In this case, one can use the blue equation to define an interpreted solution
f_A: A-> A

One example of how this function works is shown at the bottom. One can use category theory to make a connection between recursion, iterated function systems, and much else besides. In the background you can see a diagram from a paper on this topic.- Lawrence S. Moss