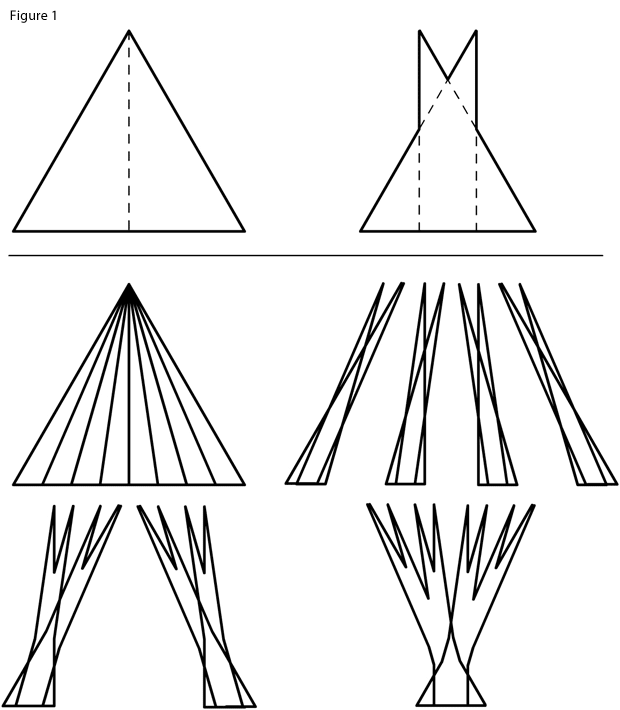
A Besicovitch set, or Kakeya set, is any set of points in Euclidean space which contains a unit line segment in every direction. Quite surprisingly, there exist Besicovitch sets with zero Lebesgue measure. Besicovitch sets of measure zero can be constructed using so called Perron trees, cf. Figure 1 below. The construction of the Perron tree itself is iterative and relies on dividing triangles into subtriangles and translating these pieces in appropriate ways. There are stronger conditions on a Besicovitch set that one can require, for instance that it contain a unit line segment which can be rotated continuously in every direction within the set. 

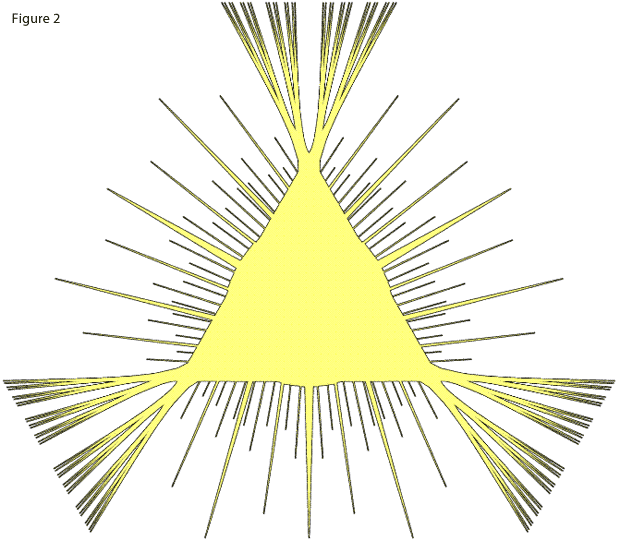
Figure 2 below shows a so-called Kakeya needle set which has this property. Again, its construction is based on Perron trees. It was shown that Kakeya needle sets can have arbitrarily small measure but never measure zero (Cunningham, 1971).- Ciprian Demeter