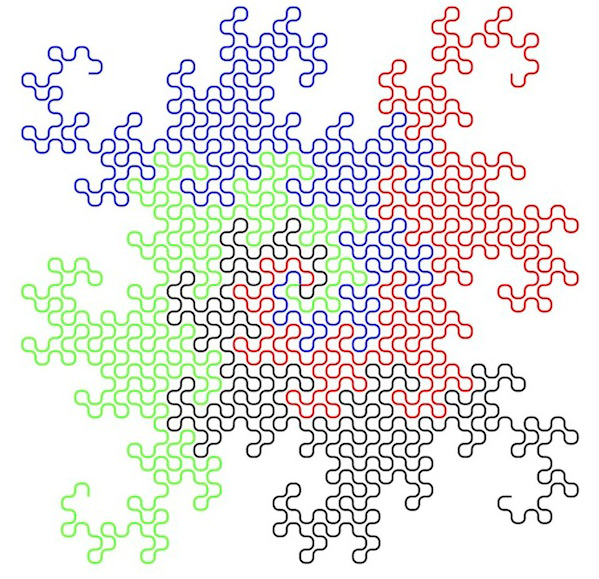
The four colored dragon curves begin in the middle and represent paths between integer points on the plane. Here is an explanation of how the red figure works. The first 2 steps are east, north (EN). To get the first 4 steps, we take EN, write it backwards to get NE, and then rotate counterclockwise to get WN. We put WN after the first two steps (EN) to get ENWN, and this is the first 4 steps on the red dragon. Similarly, the first 8 steps will be ENWNWSWN.

The other colors work the same way, but with different starting directions. What you see are the first 512 steps for each color, with all corners rounded a bit.

The four dragon curves never cross themselves or each other. Evern more surprising: when extended forever, the dragon curves would pass through every integer segment in the plane exactly once.

The infinite sequences of directions are examples of automatic sequences; the name “automatic” comes from “automaton”, a computational device with finitely many states but no memory. The nth term in the each dragon sequence is the output of an automaton whose input is the binary expansion of n. Automatic sequences have connections to continued fractions, number theory, formal language theory, and physics.

References

Most sources credit the discovery of the dragon curve to John Heighway, a physicist at NASA.

The paper that proves its properties is Chandler Davis and Donald Knuth, ”Number representations and dragon curves”, J. Recreational Math 3 (1970) 61–81 and 133-149.

It was popularized in one of Martin Gardner’s columns from Scientific American and reproduced in his book Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, 1978.

Finally, the main reference on automatic sequences is the book with that name by Jean-Paul Allouche and Jeffrey Shallit, published by Cambridge University Press in 2003. - Larry Moss