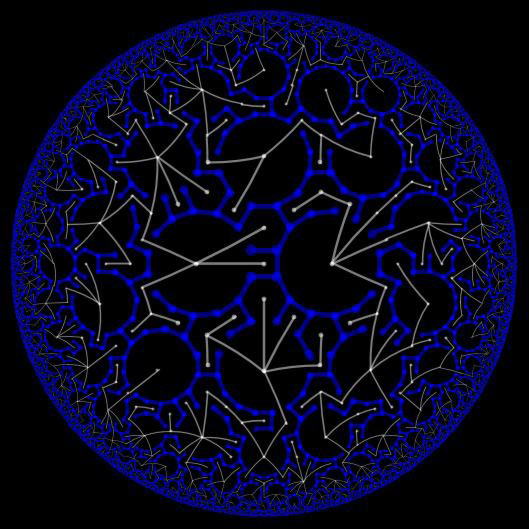
This shows two random spanning forests, one on a Cayley graph of the (2, 3, 7)-triangle tessellation of the hyperbolic plane, and the other on its plane dual. These arise as limits of uniformly random spanning trees in finite graphs, a topic going back to Kirchhoff that has deep connections to random walks and potential theory. It is also connected to \( l^2\)-Betti numbers of groups.- Russell Lyons