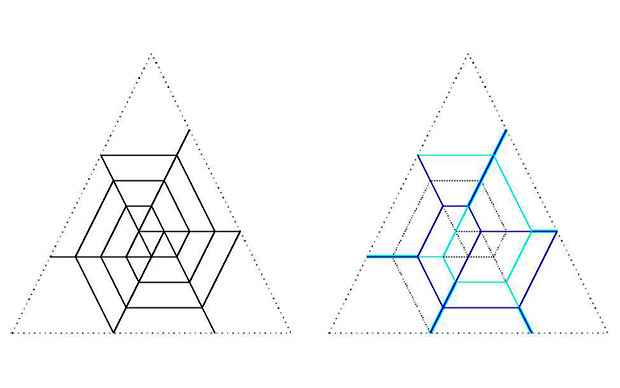
Assume you plan a roof over a triangular building with sides equal to 11 yards. Each side of the building allows only two peaks, producing a pattern of 4-4-3 yards on each side. You would also require that the lines indicating "hips" and "valleys" (preferably no valleys) should be parallel to the sides of the triangle. It turns out in this case that, once you decided the height of the roof on the three sides, the entire plan is uniquely determined, and the "hips" and "valleys" will follow the lines indicated in black on the first figure. It is possible that not all lines will be needed, and the blue and cyan lines on the second figure indicate two possibilities with minimal lines. (There are 4 more, obtained from these by rotations of 120 degrees.) 

These kinds of pictures are relevant in certain questions about the relative position of subspaces of a finite-dimensional vector space. Particularly, the decomposition of the picture on the left into six minimal "roof lines" is essential in solving intersection problems related with the Littlewood-Richardson rule.- Hari Bercovici