The Clebsch Diagonal Surface partly shown above belongs to one of the 45 families of (possibly singular) cubic surfaces in real projective 3-space. A few of the 27 straight lines that live on this surface are also drawn. After the mid 1800's, the structure and arrangement of the lines in a cubic surface were understood and applied to a number of problems in algebraic geometry by mathematicians such as Cremona, Salmon, Schläfli, Segre and Steiner.

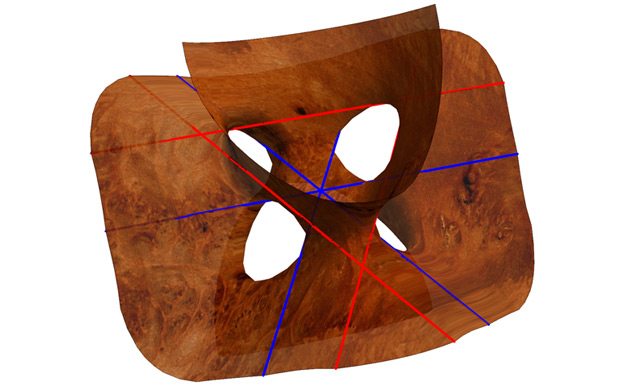
More recently, geometers have studied the invariant differential properties of algebraic surfaces. For instance, it is not immediately obvious from inspection that this surface has regions of nonnegative curvature. However, the arrangement of the straight lines on these surfaces can be used to show this. In this example, the three blue lines intersect in a common point, called an Eckardt point. The fact that lines on a surface are asymptotic directions for the second fundamental form force such triple intersections to be points of zero curvature. One advantage to this approach is that the arrangement of the lines remains topologically invariant under certain deformations of the surface.- Chris Connell