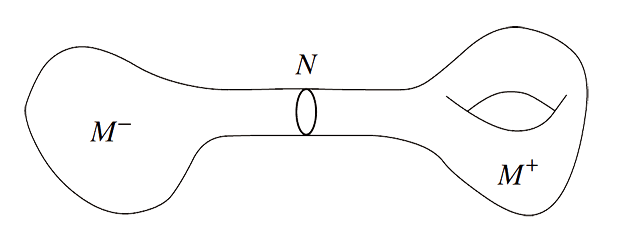
Below is an example of a picture, called a dogbone, frequently seen in mathematical articles about cut-and-paste problems in analysis on manifolds. 

It illustrates the mechanism whereby a solution or, better, the space of solutions to some geometric differential equation on a manifold M (the moduli space of M) can be understood in terms of a decomposition of M as a union of two pieces, and M^-, along a separating hypersurface N. 

A neighborhood of N is called the neck. By stretching the neck until it is very, very long (ouch!) one can understand properties of the moduli space of M in terms of information coming from the pieces M^+ and M^-. This technique has been spectacularly useful in 4-dimensional topology, for example leading to many constructions of 4-dimensional manifolds which are topologically equivalent but smoothly different.- Paul Kirk